The honeycomb conjecture states that a regular hexagonal grid is the best way to divide a surface into regions of equal area with least total perimeter:

The first recorded instance of this conjecture was made by Marcus Terentius Varro in 36 BC. Then, some 2000 years later, Thomas Hales proved in 1999 that this conjecture is true.
But can the results of the 2D honeycomb conjecture be extended to 3D? Honey bees seem to think so - their cells are based on the hexagon, as indicated by the left end of this honeycomb cell:
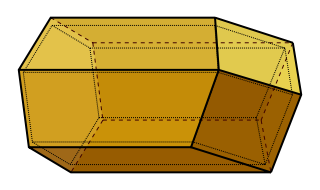
The ingeniously shaped right end allows multiple cells to tessellate efficiently in 3-space, as shown:
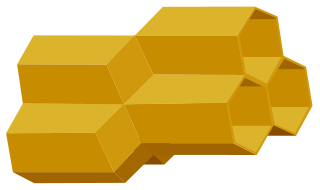
But is this the most efficient means of partitioning space into cells of equal volume with least surface area? In 1887, Lord Kelvin surmised that the following shape, known as the Kelvin structure, is optimal:
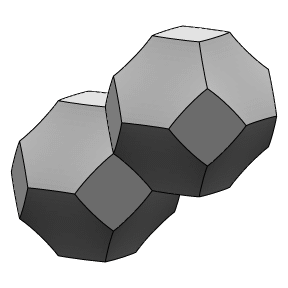
For over a century, no one could improve upon this partition of space. Then in 1993, Denis Weaire and Robert Phelan came up with a partition of space into two kinds of cells (of equal volume, of course) that beat Kelvin's partition by 0.3% in area. This partition, known as the Weaire–Phelan structure, is shown here:
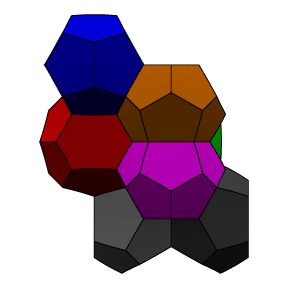
That being said, if we assume that worker bee larvae are all the same size and, therefore, that the cells for said larvae must be identical, then the Kelvin structure is the most efficient (known) means of partitioning space into identical cells of equal volume with least surface area.
There is just one problem with this result - both the Kelvin and Weaire–Phelan structures assume infinitely thin walls. This, then, begs the question - what would happen if we could increase the parameter of wall thickness from zero (infinitely thin) to some realistic thickness? Interestingly, this can be accomplished experimentally using foams (i.e., soap bubbles). A dry foam is one that has so little liquid that the walls may be regarded as having negligible thickness. A wet foam, on the other hand, is one that has enough liquid to make wall thickness appreciable (i.e., wall thickness increases as liquid is added). The following description, from Foams and Honeycombs, sums this up nicely:
The full honeycomb consists of two layers of cells, stacked together so that the caps of one layer fit into the gaps of the other, like a jigsaw puzzle. For many years it was believed that this was the best two-layer arrangement, but in 1964 the Hungarian mathematician L. Fejes Tóth showed that a hexagonal cell capped off by part of a truncated octahedron would produce a tiny saving. Tóth pointed out, however, that the bees could have excellent reasons for choosing a slightly less efficient structure. Because the honeycomb walls have a definite thickness, it is not clear that Tóth's structure would indeed be an improvement. In that respect, the honeycomb is more like a wet foam than a dry foam. Recently, Weaire and Phelan undertook to construct two-layer foams with equal-sized bubbles, and they found that the dry foams did take on Tóth's pattern. But when they gradually added liquid, they wrote, something "quite dramatic" happened: The structure suddenly switched over to the bees' configuration. It seems, then, that the bees got it right after all.
Although suggestive of an actual honeycomb, the lamp's shade is made from thin-walled tubing (not hexagonal prisms):

In this case, the most efficient means of packing such circular tubes is based on the regular hexagonal grid, as discussed in Oval Table Mathematics.